In this article, we will look at a famous algorithm in Graph Theory, Tarjan Algorithm. We will also look at an interesting problem related to it, discuss the approach and analyze the complexities.
Tarjan’s Algorithm is mainly used to find Strongly Connected Components in a directed graph. A directed graph is a graph made up of a set of vertices connected by edges, where the edges have a direction associated with them. A Strongly Connected Component in a graph is basically a self contained cycle within a directed graph where from each vertex in a given cycle we can reach every other vertex in that cycle.
Let us understand this with help of an example, consider this graph:
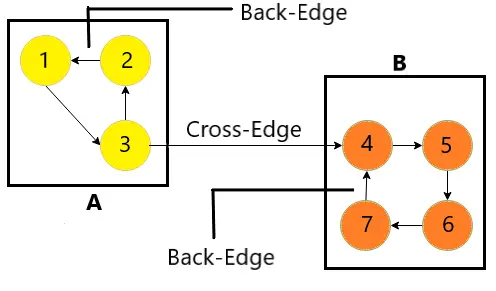
In the above graph, the box A and B show the SCC or Strongly Connected Components of the graph. Let us look at a few terminologies before explaining why the above components are SCC.
- Back-Edge: So an edge of nodes (u,v) is a Back-Edge, if the edge from u to v has Descendent-Ancestor relationship. The node u is the descendant node and node v is the ancestor node. In this case, it results in a cycle and is important in forming a Strongly Connected Component.
- Cross-Edge: An edge (u,v) is a Cross-Edge, if the edge from the u to v has no Ancestor-Descendent relationship. They are not responsible for forming a SCC. They mainly connect two SCC’s together.
- Tree-Edge: If an edge (u,v) has a Parent-Child relationship such an edge is Tree-Edge. It is obtained during the DFS traversal of the tree which forms the DFS tree of the graph.
Explanation:
So, in the above graph edges -> (1 , 3), (3 , 2), (4 , 5), (5 , 6), (6 , 7) are the tree edges because they follow the Parent-Child Relationship. Edges -> (2 , 1) and (7 , 4) form the back edges because from node 2 (Descendent) we go back to 1 (Ancestor) completing a cycle (1->3->2). Similarly, from edge 7 we go back to 4 completing a cycle ( 4-> 5 -> 6 ->7). Hence the components (1,3,2) and (4,5,6,7) are the Strongly Connected Components of the graph. The edge (3 , 4) is a Cross edge because it follows no such relationship and connects the two SCC’s together.
Note: A Strongly Connected Component in a graph must have a Back-Edge to its head node.
Tarjan’s Algorithm
Now let us see how Tarjan’s Algorithm will help us find a Strongly Connected Component.
- The idea is to do a Single DFS traversal of the graph which produces a DFS tree.
- Strongly Connected Components are the subtrees of the DFS tree. If we find the head of each subtrees, we can get access to all the nodes in the subtree which is one SCC, then we can print the SCC including the head.
- We will consider only the tree edges and back edges while traversing, we ignore the cross edges as it separates one SCC from another.
So now, let us look how to implement the above steps. We are going to assign each node a time value for when it is visited or discovered. At root or start node Time value is 0. For every node in the graph, we assign a tuple with two time values: Disc and Low.
Disc: This indicates the time for when a particular node is discovered or visited during DFS traversal. For each node we increase the Disc time value by 1.
Low: This indicates the node with lowest discovery time accessible from a given node. If there is a back edge then we update the low value based on some conditions. The maximum value Low for a node can be assigned is equal to the Disc value of that node since the minimum discovery time for a node is the time to visit/discover itself.
Note: The Disc value once assigned will not change while we keep on updating the low value traversing each node. We will discuss the condition next.
Implementation in Java
Step 1:
We use a Map (Hash-Map) to store the graph nodes and edges. The Key of map stores the nodes and in the value we have a list which represents the edges from that node. For the Disc and Low we use two integer arrays of size same as a number of vertices. We fill both the arrays with -1, to indicate no nodes are visited initially. We use a Stack (for DFS) and a Boolean array inStack to check whether an already discovered node is present in our Stack in O(1) time as checking in the stack will be a costly operation (O(n)).
Step 2:
So, for each node we process we add it into our stack and mark true in the array inStack. We maintain a static Timer variable initialized to 0. If for an edge (u,v) if v node is already present in stack, then it is a back edge and (u,v) pair is Strongly Connected. So we change the low value as :
if(Back-Edge) then Low[u] = Min ( Low[u] , Disc[v] ).
After visiting this node on returning the call to its parent node we will update the Low value for each node to ensure that Low value remains the same for all nodes in the Strongly Connected Component.
Step 3:
Now if for an edge (u,v) if v node is not present in stack then it is a tree edge or a neighboring edge. In such case, we update the low value for that particular node as :
if (Tree-Edge) then Low[u] = Min ( Low[u] , Low[v] ).
We determine the head or start node of each SCC when we get a node whose Disc[u] = Low[u], such a node is the head node of that SCC. Every SCC should have such a node maintaining this condition. After this, we just print the nodes by popping them out of the stack marking the inStack as false for each popped value.
Note: A Strongly Connected Component must have all its low values same. We will print the nodes in reverse order.
Now, let us look at the code for this in Java:
import java.util.*;
public class File
{
static HashMap<Integer,List<Integer>> adj=new HashMap<>();
static int Disc[]=new int[8];
static int Low[]=new int[8];
static boolean inStack[]=new boolean[8];
static Stack<Integer> stack=new Stack<>();
static int time = 0;
static void DFS(int u)
{
Disc[u] = time;
Low[u] = time;
time++;
stack.push(u);
inStack[u] = true;
List<Integer> temp=adj.get(u); // get the list of edges from the node.
if(temp==null)
return;
for(int v: temp)
{
if(Disc[v]==-1) //If v is not visited
{
DFS(v);
Low[u] = Math.min(Low[u],Low[v]);
}
//Differentiate back-edge and cross-edge
else if(inStack[v]) //Back-edge case
Low[u] = Math.min(Low[u],Disc[v]);
}
if(Low[u]==Disc[u]) //If u is head node of SCC
{
System.out.print("SCC is: ");
while(stack.peek()!=u)
{
System.out.print(stack.peek()+" ");
inStack[stack.peek()] = false;
stack.pop();
}
System.out.println(stack.peek());
inStack[stack.peek()] = false;
stack.pop();
}
}
static void findSCCs_Tarjan(int n)
{
for(int i=1;i<=n;i++)
{
Disc[i]=-1;
Low[i]=-1;
inStack[i]=false;
}
for(int i=1;i<=n;++i)
{
if(Disc[i]==-1)
DFS(i); // call DFS for each undiscovered node.
}
}
public static void main(String args[])
{
adj.put(1,new ArrayList<Integer>());
adj.get(1).add(3);
adj.put(2,new ArrayList<Integer>());
adj.get(2).add(1);
adj.put(3,new ArrayList<Integer>());
adj.get(3).add(2);
adj.get(3).add(4);
adj.put(4,new ArrayList<Integer>());
adj.get(4).add(5);
adj.put(5,new ArrayList<Integer>());
adj.get(5).add(6);
adj.put(6,new ArrayList<Integer>());
adj.get(6).add(7);
adj.put(7,new ArrayList<Integer>());
adj.get(7).add(4);
findSCCs_Tarjan(7);
}
}
Output:
SCC is: 7 6 5 4 SCC is: 2 3 1
The code is written for the same example as discussed above, you can see the output showing the Strongly Connected Components in reverse order since we use a Stack. Now let us look at the complexities of our approach.
Time Complexity: We are basically doing a Single DFS Traversal of the graph so time complexity will be O( V+E ). Here, V is the number of vertices in the graph and E is the number of edges.
Space Complexity: We at the most store the total vertices in the graph in our map, stack, and arrays. So, the overall complexity is O(V).
So that’s it for the article you can try out different examples and execute the code in your Java Compiler for better understanding.
Let us know any suggestions or doubts regarding the article in the comment section below.
The post Tarjan’s Algorithm with Implementation in Java appeared first on The Crazy Programmer.
from The Crazy Programmer https://ift.tt/3vYOXew
Comments
Post a Comment