In this article we look into another problem related to binary trees. Given a binary tree we have to print the Right View. We will discuss the approaches to solve this problem with their implementations and code. Along with this we will also look into the time and space complexities of our approaches.
By right view of binary tree we mean the nodes visible to us when the tree is viewed from the right side. In other words, the nodes which are present at the last of each level, the root being the first level.
Let us consider this binary tree:
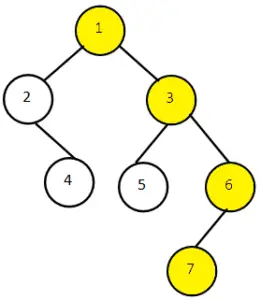
The Right View of this binary tree will give output: 1 3 6 7.
The nodes present in right view are marked in the figure. We start from the root node 1 at level 1 then we go down each level printing the last node present at each level. At level 2 node 3 is the last node so print it, at level 3 node 6 and at the last level 4 node 7 is the only node.
Note: If a level contains only one node then that node is a part of our Right View.
Input:
15 --level 1
/ \
10 35 --level 2
/ / \
5 30 45 --level 3
/
20 --level 4
Output: 15 35 45 20
Approach 1 (Recursive Approach)
We traverse the tree in a way that we keep track of current level by passing a max_level variable by reference to each recursive call or maintain a static variable so to keep track of the maximum level reached. When we process the current node we check if it’s level is more than max level till now. If current node’s level is greater than max_level we print it and update max level with current node’s level. Otherwise, we traverse for the Right Subtrees at first then the Left subtrees. Traversing right subtrees first help us print the last node of each level.
Below is the implementation of above in Java:
// class to construct each node of tree
class Node
{
int data;
Node left,right;
public Node(int data)
{
this.data=data;
left=null;
right=null;
}
}
/* Class to print the Right view and construct Tree*/
class Tree
{
Node root;
static int max_level = 0;
// recursive function to print Right view
void rightViewHelper(Node node, int current_level)
{
// Base Case
if (node == null)
return;
// If this is the last node of its level
if (max_level < current_level) {
System.out.print(" " + node.data);
max_level = current_level;
}
// Recur for Right subtrees then left subtrees
rightViewHelper(node.right,current_level + 1);
rightViewHelper(node.left,current_level + 1);
}
// A wrapper over Helper Function
void rightView()
{
rightViewHelper(root, 1);
}
public static void main(String args[])
{
/* creating a binary tree and entering the nodes */
Tree tree = new Tree();
tree.root = new Node(15);
tree.root.left = new Node(10);
tree.root.left.left=new Node(5);
tree.root.right = new Node(35);
tree.root.right.left = new Node(30);
tree.root.right.left.left = new Node(20);
tree.root.right.right = new Node(45);
tree.rightView();
}
}
Output:
15 35 45 20
Time Complexity: We do a traversal of all nodes in tree so the complexity is O (n).
Space Complexity: We call the function rightViewHelper() for each node so if System stack space is considered the complexity is O (n).
Approach 2 (Iterative Approach Using Queue)
We use Level Order Traversal technique. We print the Right-most node at each level. At first, we are going to enqueue root node in a Queue of type Node. After this we enqueue left child and right child of the current node. The order of insertion of child node does not matter here. While processing each node if it is the last node at that level we print it.
import java.util.*; //To use Queue interface implemented using Linked List Class
public class RightView
{
// Binary tree node
static class Node //Inner Class
{
int data;
Node left,right;
public Node(int data)
{
this.data = data;
this.left = null;
this.right = null;
}
}
// function to print right view of binary tree
static void rightView(Node root)
{
if (root == null)
return;
Queue<Node> q = new LinkedList<>();
q.add(root); //we add the root first.
while (!q.isEmpty())
{
// number of nodes at current level
int count = q.size();
// Traverse all nodes of current level
for (int i = 0; i < count; i++)
{
Node curr = q.poll(); //current node
// Print the left most element at
// the level
if (i == count-1)
System.out.print(curr.data + " ");
// Add left child node to queue
if (curr.left != null)
q.add(curr.left);
// Add right child node to queue
if (curr.right != null)
q.add(curr.right);
}
}
}
// Driver code
public static void main(String[] args)
{
// construct binary tree as shown in above diagram
Node root = new Node(15);
root.left = new Node(10);
root.left.left=new Node(5);
root.right = new Node(35);
root.right.left = new Node(30);
root.right.left.left = new Node(20);
root.right.right = new Node(45);
System.out.println("The Right View of the Binary Tree is: ");
System.out.println();
rightView(root);
}
}
Output:
The Right View of the Binary Tree is: 15 35 45 20
Time Complexity: We do Level by Level traversal of all nodes so the complexity is O (n) where n is the number of nodes in a Binary tree.
Space Complexity: The Queue we use will at most store the nodes present at a level so the complexity will be O (W), W is the Width of a Binary Tree or Maximum of Nodes present at all levels of Binary tree, not O (n).
That’s it for the article you can try and execute the program in your local IDE or Java online compiler to see the output.
Comment down below to ask your doubts if any.
The post Right View of Binary Tree in Java appeared first on The Crazy Programmer.
from The Crazy Programmer https://ift.tt/3jNxiB0
Comments
Post a Comment